1 Introduction

The RDHonest-vStata package implements estimates and confidence intervals (CIs) from Armstrong and Kolesár (2018) and Armstrong and Kolesár (2020) for regression discontinuity (RD) in Stata. This vignette describes some of the functionality. Section 2 discusses sharp RD. Section 3 discusses fuzzy RD. Section 4 discusses some extensions that are not currently implemented in the RDHonest-vStata package along with references to other software packages that implement them when applicable.

2 Sharp RD

To begin, we’ll illustrate using elections data from Lee (2008).

. clear all

. macro drop _all

. webuse set "https://raw.githubusercontent.com/tbarmstr/RDHonest-vStata/master/data"
(prefix now "https://raw.githubusercontent.com/tbarmstr/RDHonest-vStata/master/data")

. webuse lee08
(Lee, D. S. (2008))

The running variable margin is margin of victory of the Democratic candidate in the previous election in percentage points. The outcome variable voteshare is the Democratic candidate’s share of the vote in the next election, in percentage points. The cutoff is 0.

2.1 Estimate and CI

The rdhonest command implements honest CIs based on local linear estimates. For illustration, let’s start with the uniform kernel.

. * uniform kernel, defaults for other options:
. *   Armstrong and Kolesár (2020) rule of thumb for M + MSE optimal bandwidth
. rdhonest voteshare margin, kernel("uni")
Using Armstrong and Kolesar (2020) rule of thumb for smoothness constant M 

Honest inference: SHARP Regression Discontinuity
──────────────────────────────────────────────────────────────────────────────
 Estimate      Maximum Bias      Std. Error      [ 95% Conf.      intervals ]
──────────────────────────────────────────────────────────────────────────────
 4.79816988    .891210516        1.57140644      1.2829887         8.31335106
──────────────────────────────────────────────────────────────────────────────
 95% One-sided Conf. intervals: (1.32222577 , Inf), (-Inf,  8.27411398)
 Bandwidth (optimized): 6.01199567 
 Number of effective observations: 728        

 Parameters:
 Cutoff: 0          
 Kernel: uniform
 Optimization criterion: MSE
 Standard error estimation method: NN
 Maximum leverage for estimated parameter: .006421319 
 Smoothness constant M (rule of thumb): .142810807 
──────────────────────────────────────────────────────────────────────────────
  Dependent variable: voteshare                               
    Running variable: margin                                  

When we use the uniform kernel, the point estimate is simply obtained by running a linear regression using a “discontinuity sample” of observations within a certain distance of the cutoff (note that the cutoff is 0 in this example, which is the default for the rdhonest command; we can specify a different cutoff using the option c()). The distance that determines the discontinuity sample is called the bandwidth. It is given in the output above, and can be obtained using the postestimation e(bandwidth):

. display e(bandwidth)
6.0119957

So, in this case, we are running a linear regression using observations where the running variable is within 6.0119957 units of the cutoff point 0. We can check that the point estimates match using Stata’s built-in commands:

. scalar bw = e(bandwidth)

. gen treat = (margin>0)

. gen treatxmargin = treat*margin

. reg voteshare treat margin treatxmargin if abs(margin)<=bw, robust

Linear regression                               Number of obs     =        728
                                                F(3, 724)         =      53.20
                                                Prob > F          =     0.0000
                                                R-squared         =     0.1832
                                                Root MSE          =     11.495

─────────────┬────────────────────────────────────────────────────────────────
             │               Robust
   voteshare │      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
       treat │    4.79817   1.614018     2.97   0.003     1.629456    7.966884
      margin │   .9246502   .3048005     3.03   0.003     .3262519    1.523049
treatxmargin │  -.0081335   .4760755    -0.02   0.986    -.9427869    .9265199
       _cons │   46.99352   1.061989    44.25   0.000     44.90857    49.07847
─────────────┴────────────────────────────────────────────────────────────────

Note that, while the point estimates match, the standard errors are slightly different. This is due to the rdhonest command defaulting to a nearest-neighbor (NN) standard error, rather than the usual EHW standard error. The NN standard error can be less conservative in certain settings, but here the two methods yield similar results.

A more striking difference is the 95% CI computed by the built-in regression command, which is slightly shorter than the one reported by rdhonest. The rdhonest command computes a bias-aware CI that explicitly takes into account the largest possible bias in a smoothness class determined by a smoothness constant \(M\). In particular, rather than assuming the specification in the above regression holds exactly, we assume that it holds only up to approximation error:

\[ \text{voteshare}_i = \tau \cdot \text{treat}_i + \beta_1 + \beta_2 \text{margin}_i + \beta_3 \text{treat}_i\cdot \text{margin}_i + \text{rem}(\text{margin}_i) + u_i \]

where \(\text{treat}_i=I(\text{margin}_i>0)\) and \(\text{rem}(\text{margin}_i)\) is the remainder term from a first order Taylor approximation of the conditional expectation function of voteshare given margin by the linear specification on either side of the cutoff point. We assume that this remainder term comes from a Taylor approximation where this conditional expectation function is twice differentiable, with second derivative bounded by \(M\). The rdhonest command allows \(M\) to be specified throught the m() option. If this option is not specified (as in the example above), it uses a rule-of-thumb from Armstrong and Kolesár (2020) that calibrates \(M\) based on a global fourth order polynomial on either side of the cutoff. The maximum bias and smoothness constant are displayed in the output for rdhonest. It can be obtained in postestimation with e(bias) and e(M).

The two-sided CI reported by rdhonest uses the critical value \(\text{cv}_{\alpha}(t)\), computed as the \(1-\alpha\) quantile of the \(|N(0,t)|\) distribution, with \(t=\frac{\text{max. bias}}{\text{se}}\):

\[ \text{estimate} \pm \text{cv}_{\alpha}\left(\frac{\text{max. bias}}{\text{se}}\right)\cdot \text{se} \]

By taking into account the maximum possible bias, this critical value ensures that the coverage of the CI is at least \(1-\alpha\). The level \(\alpha\) is set using the option alpha() and defaults to \(.05\). We refer to this as a fixed-length CI, since it depends only on the standard error and the smoothness constant \(M\). Note that one could also add and subtract \(\text{max. bias} + z_{1-\alpha/2}\cdot \text{se}\) to form the CI. Indeed, the one-sided CIs reported by rdhonest take this form: the lower endpoint of the lower one-sided CI is \[ \text{estimate} - \text{max. bias} - z_{1-\alpha}\cdot \text{se} \] where \(z_{1-\alpha}\) is the \(1-\alpha\) quantile of the \(N(0,1)\) distribution. However, in the two-sided case, the above construction is less conservative.

2.2 Interpreting the Smoothness Assumption and Honesty Requirement

The identifying assumption in sharp RD is that the latent conditional expectation functions for treated and untreated outcomes are smooth. The smoothness class described above formalizes this in a way that allows for valid inference and guarantees on estimation error. The CIs reported by rdhonest are honest in the sense that coverage is close to the nominal level or better for all functions in this class once the sample size is large enough. In addition, since these CIs use finite-sample bounds on bias, the only thing needed for good finite-sample coverage is accuracy of the normal approximation. In particular, they are valid with discrete covariates.

Some users may be more familiar with “pointwise-in-the-underlying-distribution” formulations of smoothness. These are used, for example, in the optimal bandwidth calculations of Imbens and Kalyanaraman (2012). For many practical purposes, the two formulations lead to similar conclusions and interpretations. For example, the mean squared error optimal bandwidth (computed by rdhonest and discussed below) turns out to have the same asymptotic formula as the one used by Imbens and Kalyanaraman (2012), with \(M\) in our setting taking the place of the second derivative (or difference in second derivatives) in Imbens and Kalyanaraman (2012). Indeed, one can loosely think of the honest CI formulation used by rdhonest as a “decision theoretically kosher” version of pointwise-in-the-underlying distribution smoothness formulations. Key practical differences are:

• The honest CI formulation used by rdhonest can be used in finite samples, thereby allowing for discrete covariates.

• The honest CI formulation treats \(M\) as a bound on the second derivative, rather than an exact value of the second derivative. This precludes higher order bias correction without further assumptions on higher derivatives. If one makes assumptions on higher order derivatives, this is done in the honest CI framework by formulating a bound \(M_{\text{higher}}\) on this derivative and optimally using this bound to form estimates and CIs.

See Section 4 of Armstrong and Kolesár (2020) for further discussion.

2.3 Choice of Bandwidth

If the bandwidth is unspecified (as in the above example) rdhonest computes the bandwidth that optimizes a given criterion for the smoothness class characterized by the bound \(M\) on the second derivative of the regression function. The criterion can be set using the option opt_criterion(). Options are MSE for mean squared error, FLCI for two-sided CI length and OCI for excess length of a one-sided CI, with MSE set as the default.

The optimization is done using an initial estimate of the conditional variance. Because rdhonest reports a robust standard error and a bias-aware CI based on this standard error, the variance estimate used to optimize the CI will be different than the one used for the reported standard error and CI.

The fact that different criteria lead to different point estimates is potentially irksome: we may want to report a point estimate that optimizes MSE, while using the FLCI option to report a CI that is as small as possible. This can be easily done by rerunning the rdhonest command with both options, but one may be hesitant to report a CI that is not centered at the reported point estimate. Fortunately, a result from Armstrong and Kolesár (2020) shows that, under standard RD asymptotics, MSE and CI length lead to very similar bandwidths, and that using the MSE optimal bandwidth to compute a bias-aware CI is still highly efficient. Let’s see how much we can reduce the length of our CI by choosing the bandwidth to minimize CI length:

. * same specification as before, but choose the bandwidth to minimize CI length
. rdhonest voteshare margin, kernel("uni") opt_criterion("FLCI")
Using Armstrong and Kolesar (2020) rule of thumb for smoothness constant M 

Honest inference: SHARP Regression Discontinuity
──────────────────────────────────────────────────────────────────────────────
 Estimate      Maximum Bias      Std. Error      [ 95% Conf.      intervals ]
──────────────────────────────────────────────────────────────────────────────
 5.14231308    .951187869        1.57124452      1.5754211         8.70920506
──────────────────────────────────────────────────────────────────────────────
 95% One-sided Conf. intervals: (1.60665797 , Inf), (-Inf,  8.67796819)
 Bandwidth (optimized): 6.18426502 
 Number of effective observations: 750        

 Parameters:
 Cutoff: 0          
 Kernel: uniform
 Optimization criterion: FLCI
 Standard error estimation method: NN
 Maximum leverage for estimated parameter: .00612847  
 Smoothness constant M (rule of thumb): .142810807 
──────────────────────────────────────────────────────────────────────────────
  Dependent variable: voteshare                               
    Running variable: margin                                  

The bandwidth, point estimate, and CI are all very similar to the ones based on the MSE optimal bandwidth above. In this case, the MSE optimal bandwidth actually leads to a slightly shorter CI than the CI optimal bandwidth. This is due to different variance estimates being used to compute the bandwidth and the CI, as described above.

The rdhonest package also includes an option to specify the bandwidth directly, through the option h(). However, this may lead to a bandwidth that is far from optimal for the smoothness constant \(M\) specified through m(), or through the default rule-of-thumb. Rather than specifying the bandwidth directly, we recommend specifying the smoothness constant \(M\) through the m() option, and letting the rdhonest command compute the optimal bandwidth. Since the optimal bandwidth depends directly on \(M\), this is equivalent to checking sensitivity of results to the bandwidth. We discuss this below.

An exception to this practice arises if the optimal bandwidth leads to a very small number of effective observations, which may lead to poor finite-sample performance of the CI due to failure of the normal approximation. One may then want to use the option h() to specify a larger bandwidth.

2.4 Sensitivity Analysis

As shown in Armstrong and Kolesár (2018), it is impossible to avoid specifying the smoothness constant \(M\), either explicitly or using auxiliary assumptions, such as the assumptions described in Armstrong and Kolesár (2020) relating a global polynomial to local smoothness that motivate the rule-of-thumb used by rdhonest as a default. We therefore recommend varying \(M\) as a form of sensitivity analysis. Since we let rdhonest compute the optimal bandwidth for each value of \(M\), this is equivalent to reporting specifications with different bandwidths.

Let’s try some other choices of \(M\) in our original specification. We’ll start with the default Armstrong and Kolesár (2020) rule-of-thumb, and then consider more optimistic (smaller) choices of \(M\), and more pessimistic (larger) choices of \(M\).

. qui rdhonest voteshare margin, kernel("uni")

. scalar M_rot = e(M)

. scalar est_rot = e(est)

. scalar HLCi_rot = e(HLCi)

. scalar h_rot = e(bandwidth)

. 
. * some other values of M to try
. scalar M01 = .1*M_rot

. scalar M05 = .5*M_rot

. scalar M2 = 2*M_rot

. scalar M10 = 10*M_rot

. 
. qui rdhonest voteshare margin, kernel("uni") m(`=M01')

. scalar est01 = e(est)

. scalar HLCi01 = e(HLCi)

. scalar h01 = e(bandwidth)

. 
. qui rdhonest voteshare margin, kernel("uni") m(`=M05')

. scalar est05 = e(est)

. scalar HLCi05 = e(HLCi)

. scalar h05 = e(bandwidth)

. 
. qui rdhonest voteshare margin, kernel("uni") m(`=M2')

. scalar est2 = e(est)

. scalar HLCi2 = e(HLCi)

. scalar h2 = e(bandwidth)

. 
. qui rdhonest voteshare margin, kernel("uni") m(`=M10')

. scalar est10 = e(est)

. scalar HLCi10 = e(HLCi)

. scalar h10 = e(bandwidth)

. 
. disp _newline "M     | bw    | est.   | lower CI | upper CI "  _newline /// 
> round(M01,.0001) " | " round(h01,.0001) " | " round(est01,.0001) " | " round(est01-HLCi01,.0001) " | " round(est01+HLCi01,.0001) _newline  ///
>  round(M05,.0001) " | " round(h05,.0001) " | " round(est05,.0001) " | " round(est05-HLCi05,.0001) " | " round(est05+HLCi05,.0001) _newline  ///
>  round(M_rot,.0001) " | " round(h_rot,.0001) " | " round(est_rot,.0001) " | " round(est_rot-HLCi_rot,.0001) " | " round(est_rot+HLCi_rot,.0001) _n
> ewline ///
>  round(M2,.0001) " | " round(h2,.0001) " | " round(est2,.0001) " | " round(est2-HLCi2,.0001) " | " round(est2+HLCi2,.0001) _newline ///
>  round(M10,.0001) " | " round(h10,.0001) " | " round(est10,.0001) " | " round(est10-HLCi10,.0001) " | " round(est10+HLCi10,.0001) 

M     | bw    | est.   | lower CI | upper CI 
.0143 | 15.0777 | 7.7854 | 5.5526 | 10.0181
.0714 | 7.9692 | 6.0282 | 3.0281 | 9.0283
.1428 | 6.012 | 4.7982 | 1.283 | 8.3134
.2856 | 4.5821 | 5.2085 | 1.4933 | 8.9236
1.4281 | 2.4064 | 10.7135 | 5.8504 | 15.5766

Note that we have used the postestimation e(HLCi) to get the half-length of the bias-aware CI, which we add and subtract from the point estimate to get our bias-aware CI.

In this case, the finding of a positive effect size is quite robust: it persists even when we take \(M\) to be 10 times the rule-of-thumb value, which corresponds to a bandwidth of about 2.4.

2.5 Kernel

While we have been using the uniform kernel so far, rdhonest also includes other kernel options, which can be specified using the kernel() option. The default is the triangular kernel:

. rdhonest voteshare margin
Using Armstrong and Kolesar (2020) rule of thumb for smoothness constant M 

Honest inference: SHARP Regression Discontinuity
──────────────────────────────────────────────────────────────────────────────
 Estimate      Maximum Bias      Std. Error      [ 95% Conf.      intervals ]
──────────────────────────────────────────────────────────────────────────────
 5.84973224    .88800705         1.36588331      2.69443541        9.00502906
──────────────────────────────────────────────────────────────────────────────
 95% One-sided Conf. intervals: (2.71504707 , Inf), (-Inf,  8.98441741)
 Bandwidth (optimized): 7.71506984 
 Number of effective observations: 764.559585 

 Parameters:
 Cutoff: 0          
 Kernel: triangular
 Optimization criterion: MSE
 Standard error estimation method: NN
 Maximum leverage for estimated parameter: .009560868 
 Smoothness constant M (rule of thumb): .142810807 
──────────────────────────────────────────────────────────────────────────────
  Dependent variable: voteshare                               
    Running variable: margin                                  

This is numerically equivalent to a weighted least squares regression, with weights decreasing linearly from \(1\) at the cutoff to \(0\) when the running variable is equal to the bandwidth:

. scalar bw = e(bandwidth)

. gen kern_wgt = (1-abs(margin/bw))*((1-abs(margin/bw))>0)

. 
. reg voteshare treat margin treatxmargin [weight=kern_wgt], robust
(analytic weights assumed)
(sum of wgt is 462.4894459116331)

Linear regression                               Number of obs     =        936
                                                F(3, 932)         =      58.63
                                                Prob > F          =     0.0000
                                                R-squared         =     0.1573
                                                Root MSE          =     11.346

─────────────┬────────────────────────────────────────────────────────────────
             │               Robust
   voteshare │      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
       treat │   5.849732   1.396805     4.19   0.000     3.108485    8.590979
      margin │   .6235424   .2295346     2.72   0.007     .1730779    1.074007
treatxmargin │   .1217772   .3545124     0.34   0.731     -.573958    .8175123
       _cons │   46.31878   .9083813    50.99   0.000     44.53607    48.10149
─────────────┴────────────────────────────────────────────────────────────────

As before, we obtain the same point estimates, but different CIs due to rdhonest explicitly taking into account bias.

The triangular kernel is used as a default due to its simplicity and high efficiency (as shown by Armstrong and Kolesár (2020), it is 97.28% efficient relative to the optimal kernel derived by Gao (2018), whereas the uniform kernel is 91.65% efficient). Indeed, here we see that the bias-aware CI based on the triangular kernel is somewhat shorter than the one based on the uniform kernel.

2.6 Discrete Running Variable

For sharp RD, the rdhonest command gives valid CIs for discrete as well as continuous running variables. This is because the worst-case bias calculation holds in finite samples, following Armstrong and Kolesár (2018). In particular, it does not require asymptotic approximations that use assumptions on the running variable. Furthermore, if observations near the cutoff are omitted in a “doughnut design,” the rdhonest command automatically takes into account additional bias from extrapolating the regression function to the cutoff point.

2.7 Estimation Weights

The estimators used by rdhonest are linear estimators: they can be written as a linear combination of the outcome \(y_i\) with weights \(w_i\) depending on the entire sample of the running variable \(x_i\):

\[ \text{estimate} = \sum_{i=1}^n w_i y_i \]

We refer to these as estimation weights. The estimation weights can be saved as a new variable using the savewgtest() option:

. * triangular kernel
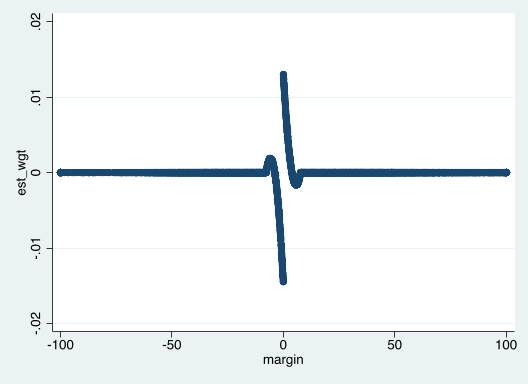
. qui rdhonest voteshare margin, savewgtest(est_wgt)

We can then plot the weights \(w_i\) against the running variable \(x_i\):

. scatter est_wgt margin

Plots of this form were popularized by Gelman and Imbens (2017). Such plots can be used to assess which values of the running variable are influential in our estimate. In particular, we see that the weights are nonzero only for observations in the discontinuity sample, where the running variable is close to the cutoff point (\(0\) in this case).

The estimation weights also play an important role in the calculation of worst-case bias used to form the bias-aware CI. To give an intuitive description of this, recall that the worst-case bias is calculated using a bound on error from a Taylor approximation at the cutoff. Choosing an estimator with estimation weights \(w_i\) that are zero for \(x_i\) far away from the cutoff (which can be done by choosing a small enough bandwidth) ensures that the approximation error is not too large. We give a more detailed discussion of how the estimation weights are used to calculate the maximum bias in the next section. This section can be skipped by readers not interested in technical details.

2.8 Calculating Maximum Bias

As discussed above, rdhonest computes bias-aware CIs based on the maximum bias under the assumption that the conditional expectation of the outcome variable given the running variable has second derivative bounded by the smoothness constant \(M\) on either side of the cutoff. This section describes the formula for maximum bias. It can be skipped by readers not interested in technical details.

For a generic running variable \(x_i\) and outcome variable \(y_i\), the smoothness class used by rdhonest amounts to the following specification, assuming for simplicity that the cutoff point is \(0\):

\[ y_i = \tau \cdot I(x_i>0) + \beta_1 + \beta_2 x_i + \beta_3 I(x_i>0)\cdot x_i + \text{rem}(x_i) + u_i. \]

The remainder term \(\text{rem}(x)\) has second derivative bounded by \(M\), and satisfies \(\text{rem}(0)=\text{rem}'(0)=0\) (since the function and its first derivative are incorporated into the parameters \(\tau\) and \(\beta\)). Assuming \(u_i\) is mean zero conditional on the \(x_i\)s, the bias of a local linear estimator with estimation weights \(w_i\), conditional on the \(x_i\)’s, is given by

\[ \sum_{i=1}^n w_i \text{rem}(x_i) \]

(this follows by unbiasedness of the local linear estimator under the “correct specification” where \(\text{rem}(x_i)=0\)). A result in Armstrong and Kolesár (2020) shows that, when the weights \(w_i\) are formed from a local linear estimator with a nonnegative kernel, the magnitude of this bias term is maximized when \(\text{rem}(x_i)=-(M/2) x_i^2\cdot \text{sign}(x_i)\):

\[ \text{max. bias} = - (M/2) \sum_{i=1}^n w_i x_i^2\cdot \text{sign}(x_i). \]

We can use this to calculate maximum bias manually, and check that this matches with the quantity used by rdhonest to compute a bias-aware CI. The rdhonest command stores the maximum bias in e(bias).

. * worst-case bias from the previous rdhonest command
. disp e(bias)
.88800705

. 
. * calculate worst-case bias manually using estimation weights saved in est_wgt
. gen worst_case_bias_summand = -(e(M)/2)*est_wgt*(margin^2)*sign(margin)

. qui summarize worst_case_bias_summand

. disp r(sum)
.88800705

2.9 Asymptotic Approximation to CI Length: the 2.18 Rule

How much wider is the bias-aware CI relative to a CI that uses the “bias-unaware” critical value 1.96 for a nominal 95% CI? Of course, we can easily check this for a given data set using rdhonest, as we’ve already done. To provide a more general answer to this question, Armstrong and Kolesár (2020) provide an asymptotic formula that holds when the running variable is continuous with a positive density. In particular, if the MSE optimal bandwidth is used and the running variable is continuously distributed with a positive density, one can approximate the bias-aware 95% CI computed by rdhonest by replacing the conventional critical value 1.96 with the number 2.18. Thus, the bias-aware CI is wider by a factor of approximately \(2.18/1.96\approx 1.11\).

Let’s see how this works with our running example:

. * compute honest CI
. qui rdhonest voteshare margin, kernel("uni")

. disp "[ " e(est) - e(HLCi) " , " e(est) + e(HLCi) " ]"
[ 1.2829887 , 8.3133511 ]

. 
. * compute asymptotic approximation using 2.18 rule
. disp "[ " e(est) - 2.18*e(se) " , " e(est) + 2.18*e(se) " ]"
[ 1.3725038 , 8.2238359 ]

The approximation is reasonably accurate in this case, leading to a slightly smaller CI, but not by much. The accuracy of this approximation might be expected given that the running variable is fairly well-behaved in this dataset. However, given that rdhonest computes worst-case bias exactly in finite-samples, there is no need to use asymptotic approximations to compute worst-case bias.

3 Fuzzy RD

We’ll illustrate the application of the rdhonest command to fuzzy RD using the data from Battistin et al. (2009).

. clear all

. macro drop _all

. webuse set "https://raw.githubusercontent.com/tbarmstr/RDHonest-vStata/master/data"
(prefix now "https://raw.githubusercontent.com/tbarmstr/RDHonest-vStata/master/data")

. webuse rcp
(Battistin, E., Brugiavini, A., Rettore, E., & Weber, G. (2009))

. gen log_cn = log(cn)

The outcome variable log_cn is consumption in logs, the treatment retired is an indicator for retirement and the running variable elig_year is the number of years since being eligible to retire. The cutoff is 0.

3.1 Estimate and CI

For fuzzy RD, the syntax is rdhonest depvar (treat = runvar). As with the sharp RD example, we’ll begin by using the uniform kernel.

. rdhonest log_cn (retired=elig_year), kernel("uni")
Using Armstrong and Kolesar (2020) rule of thumb for smoothness constant M 

Honest inference: FUZZY Regression Discontinuity
──────────────────────────────────────────────────────────────────────────────
 Estimate      Maximum Bias      Std. Error      [ 95% Conf.      intervals ]
──────────────────────────────────────────────────────────────────────────────
 -.154754788   .094148696        .09951997       -.412793464       .103283889
──────────────────────────────────────────────────────────────────────────────
 95% One-sided Conf. intervals: (-.412599268, Inf), (-Inf,  .103089693)
 First-stage estimate: .323809965 
 Bandwidth (optimized): 5          
 Number of effective observations: 5018       

 Parameters:
 Cutoff: 0          
 Kernel: uniform
 Optimization criterion: MSE
 Standard error estimation method: NN
 Maximum leverage for estimated parameter: .000763565 
 Smoothness constant M (first-stage, rule of thumb): .008178929 
 Smoothness constant M (reduced-form, rule of thumb): .002849524 
──────────────────────────────────────────────────────────────────────────────
  Dependent variable: log_cn                                  
    Running variable: elig_year                               
  Treatment variable: retired                                 

The estimate is the ratio of local linear estimators for the discontinuity at the cutoff in a reduced form and first stage regression. With the uniform kernel, this is numerically equivalent to running an instrumental variables regression controlling for a linear trend on either side of the cutoff, with an indicator for eligibility as the instrument:

. scalar bw = e(bandwidth)

. gen eligible = (elig_year>0)

. gen eligiblexelig_year = eligible*elig_year

. ivreg log_cn (retired=eligible) elig_year eligiblexelig_year if abs(elig_year<=bw), robust

Instrumental variables (2SLS) regression        Number of obs     =     19,245
                                                F(3, 19241)       =     229.84
                                                Prob > F          =     0.0000
                                                R-squared         =     0.0525
                                                Root MSE          =      .4489

───────────────────┬────────────────────────────────────────────────────────────────
                   │               Robust
            log_cn │      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
───────────────────┼────────────────────────────────────────────────────────────────
           retired │  -.3194117    .044604    -7.16   0.000    -.4068394    -.231984
         elig_year │   .0123859   .0005108    24.25   0.000     .0113847    .0133871
eligiblexelig_year │  -.0136842   .0069804    -1.96   0.050    -.0273664   -1.94e-06
             _cons │   9.912645   .0099964   991.62   0.000     9.893051    9.932239
───────────────────┴────────────────────────────────────────────────────────────────
Instrumented:  retired
Instruments:   elig_year eligiblexelig_year eligible
────────────────────────────────────────────────────────────────────────────────────

As with the sharp RD example, the point estimate is the same, but the confidence interval differs since the rdhonest command uses a bias-aware critical value that takes into account possible approximation error. Here, we have two reduced form IV equations with possible specification error, one for the outcome variable \(\log (\text{cn}_i)\) and a first-stage equation for the treatment variable \(\text{retired}_i\):

\[\begin{align*} \log (\text{cn}_i) = &\tau_{\text{outcome}} \cdot \text{eligible}_i + \beta_1 + \beta_2 \text{elig\_year}_i + \beta_3 \text{eligible}_i\cdot \text{elig\_year}_i \\ & + \text{rem}_{\text{outcome}}(\text{elig\_year}_i) + u_i \\ \text{retired}_i = &\tau_{\text{first-stage}} \cdot \text{eligible}_i + \gamma_1 + \gamma_2 \text{elig\_year}_i + \gamma_3 \text{eligible}_i\cdot \text{elig\_year}_i \\ &+ \text{rem}_{\text{first-stage}}(\text{elig\_year}_i) + v_i \end{align*}\]

The fuzzy RD parameter is

\[ \tau_{\text{FRD}} = \frac{\tau_{\text{outcome}}}{\tau_{\text{first-stage}}} \]

The rdhonest command takes into account the largest possible asymptotic bias of the estimate over a smoothness class for the reduced form outcome equation as well as the first stage equation. The smoothness class is the same one used for sharp RD: we assume that the remainder term \(\text{rem}()\) comes from a first-order Taylor approximation at the cutoff (in this case \(0\)), where the second derivative is bounded by a smoothness constant \(M\). The smoothness constant \(M_{\text{outcome}}\) for the reduced form outcome equation is allowed to differ from the smoothness constant \(M_{\text{first-stage}}\) for the first-stage equation. These can be specified through the option m(M_outcome M_firststage). If no options are specified, then rdhonest applies the rule-of-thumb from Armstrong and Kolesár (2020) to each of the equations (reduced form outcome equation and first-stage equation) separately to specify \(M_{\text{outcome}}\) and \(M_{\text{first-stage}}\).

3.2 Sensitivity Analysis and Choice of Bandwidth

As with sharp RD, the rdhonest command optimizes the bandwidth for a given criterion specified by opt_criterion() if no bandwith is specified, with MSE as the default optimality criterion. For the same reasons described above for sharp RD, we recommend varying \(M_{\text{outcome}}\) and \(M_{\text{first-stage}}\) and letting rdhonest optimize the bandwidth, rather than setting the bandwidth directly (unless the optimized value leads to a very small number of effective observations such that normal approximation may not work well). Note that while, in principle, one could further improve efficiency by using different bandwidths for the first-stage and reduced form outcome equations, this option is not currently supported by the rdhonest package.

Let’s try some other values of \(M_{\text{outcome}}\) and \(M_{\text{first-stage}}\). We’ll start with the rule-of-thumb values used by default in the specification above, and multiply them by \(1/2\) and \(2\). We can extract these using e(M) for the outcome and e(M_fs) for the first stage.

. qui rdhonest log_cn (retired=elig_year), kernel("uni")

. scalar M_outcome_rot = e(M)

. scalar M_firststage_rot = e(M_fs)

. 
. scalar M_outcome_05 = .5*M_outcome_rot

. scalar M_firststage_05 = .5*M_firststage_rot

. scalar M_outcome_2 = 2*M_outcome_rot

. scalar M_firststage_2 = 2*M_firststage_rot

. 
. qui rdhonest log_cn (retired=elig_year), kernel("uni") m(`=M_outcome_rot' `=M_firststage_rot')

. scalar est_rot = e(est)

. scalar HLCi_rot = e(HLCi)

. scalar h_rot = e(bandwidth)

. 
. qui rdhonest log_cn (retired=elig_year), kernel("uni") m(`=M_outcome_05' `=M_firststage_05')

. scalar est05 = e(est)

. scalar HLCi05 = e(HLCi)

. scalar h05 = e(bandwidth)

. 
. qui rdhonest log_cn (retired=elig_year), kernel("uni") m(`=M_outcome_2' `=M_firststage_2')

. scalar est2 = e(est)

. scalar HLCi2 = e(HLCi)

. scalar h2 = e(bandwidth)

. 
. disp _newline "M_outcome | M_firststage | bw | est.   | lower CI | upper CI "  _newline /// 
> round(M_outcome_05,.0001) "     | " round(M_firststage_05,.0001) "        | " round(h05,.0001) "  | " round(est05,.0001) " | " round(est05-HLCi05,
> .0001) " | " round(est05+HLCi05,.0001) _newline  ///
> round(M_outcome_rot,.0001) "     | " round(M_firststage_rot,.0001) "        | " round(h_rot,.0001) "  | " round(est_rot,.0001) " | " round(est_rot
> -HLCi_rot,.0001) " | " round(est_rot+HLCi_rot,.0001) _newline  ///
> round(M_outcome_2,.0001) "     | " round(M_firststage_2,.0001) "        | " round(h2,.0001) "  | " round(est2,.0001) "  | " round(est2-HLCi2,.0001
> ) "  | " round(est2+HLCi2,.0001)

M_outcome | M_firststage | bw | est.   | lower CI | upper CI 
.0014     | .0041        | 7  | -.0772 | -.2716 | .1172
.0028     | .0082        | 5  | -.1548 | -.4128 | .1033
.0057     | .0164        | 4  | -.244  | -.609  | .121

3.3 Bias and Variance Calculations for Fuzzy RD

For fuzzy RD, the point estimate is given by \(\hat\tau_{\text{FRD}} = \frac{\hat\tau_{\text{outcome}}}{\hat\tau_{\text{first-stage}}}\) where \(\hat\tau_{\text{outcome}}\) and \(\hat\tau_{\text{first-stage}}\) are local linear estimates of the discontinuity \(\tau_{\text{outcome}}\) in the reduced form outcome equation and the discontinuity \(\tau_{\text{first-stage}}\) in the first stage respectively. The rdhonest command uses the delta method approximation

\[ \hat\tau_{\text{FRD}} - \tau_{\text{FRD}} \approx \hat\tau_{\text{outcome}} - \tau_{\text{outcome}} - \tau_{\text{FRD}} (\hat\tau_{\text{FRD}} - \tau_{\text{FRD}}) \]

The bias and variance are then computed in the same way as sharp RD. For example, the maximum bias is computed as

\[ \text{max. bias}_{\text{outcome}} + |\tau_{\text{FRD}}| \cdot \text{max. bias}_{\text{first-stage}} \]

where \(\text{max. bias}_{\text{outcome}}\) and \(\text{max. bias}_{\text{first-stage}}\) are the maximum bias for each of the reduced form equations, computed in the same way as for sharp RD. Since \(\tau_{\text{FRD}}\) is unknown, rdhonest uses an initial value specified by the option t0() to calculate bias and variance for bandwidth optimization for the estimate (the default is \(0\)). Then, the point estimate \(\hat\tau_{\text{FRD}}\) is used in the above formula to compute maximum bias when constructing the CI. Thus, the CI is asymptotically valid regardless of the initial value specified by t0(), but the bandwidth is optimal only if a consistent estimate of \(\tau_{\text{FRD}}\) is plugged into t0(). See Armstrong and Kolesár (2020) for details.

Note that the default option t0(0) leads to an asymptotically efficient bandwidth choice only when \(\tau_{\text{FRD}}=0\). One can obtain an asymptotically efficient estimate by rerunning the command with t0(`=e(est)'):

. qui rdhonest log_cn (retired=elig_year), kernel("uni")

. 
. rdhonest log_cn (retired=elig_year), kernel("uni") t0(`=e(est)')
Using Armstrong and Kolesar (2020) rule of thumb for smoothness constant M 

Honest inference: FUZZY Regression Discontinuity
──────────────────────────────────────────────────────────────────────────────
 Estimate      Maximum Bias      Std. Error      [ 95% Conf.      intervals ]
──────────────────────────────────────────────────────────────────────────────
 -.243983953   .078178872        .126823328      -.533125871       .045157965
──────────────────────────────────────────────────────────────────────────────
 95% One-sided Conf. intervals: (-.530768636, Inf), (-Inf,   .04280073)
 First-stage estimate: .309048375 
 Bandwidth (optimized): 4          
 Number of effective observations: 3677       

 Parameters:
 Cutoff: 0          
 Kernel: uniform
 Optimization criterion: MSE
 Standard error estimation method: NN
 Maximum leverage for estimated parameter: .000989375 
 Smoothness constant M (first-stage, rule of thumb): .008178929 
 Smoothness constant M (reduced-form, rule of thumb): .002849524 
──────────────────────────────────────────────────────────────────────────────
  Dependent variable: log_cn                                  
    Running variable: elig_year                               
  Treatment variable: retired                                 

While this may lead to a some improvement in CI length, this may come at the expense of finite sample performance, due to the extra uncertainty introduced by using the initial estimate to compute the bias-variance tradeoff. This is similar to the tradeoff between asymptotic optimality and finite sample performance with feasible generalized least squares or two-step generalized method of moments. For this reason, the default implementation simply uses \(0\) for the t0() option.

3.4 Discrete Running Variables and Weak First Stage

The delta method approximation described above relies on asymptotics. This is not an issue for discrete running variables per se, since the formulas for \(\text{max. bias}_{\text{outcome}}\) and \(\text{max. bias}_{\text{first-stage}}\) that the rdhonest command plugs into this delta method approximation are valid in finite samples, including a discrete running variable. However, the delta method approximation will break down if the estimate of \(\tau_{\text{FRD}}\) is inconsistent, which will be relevant when the number of support points of the running variable is small, or in “doughnut designs,” where observations with the running variable near the cutoff are discarded. Furthermore, this approximation will not work under “weak instrument” asymptotics where \(\tau_{first-stage}\) is zero or small relative to the sample size.

To compute honest CIs with better finite sample performance in settings where such concerns are relevant, one can apply an Anderson-Rubin approach with honest CIs for sharp RD, as proposed by Noack and Rothe (2019). In particular, to test the null hypothesis \(H_0:\tau_{\text{FRD}}=\tau_{\text{null}}\) using this method, one forms the outcome \(\text{outcome}_i - \tau_{\text{null}} \cdot \text{treat}_i\) and runs rdhonest with \(M\) set to \(M_{\text{outcome}}+|\tau_{\text{null}}|\cdot M_{first-stage}\) using the m() option. One can then do this for a grid of values of \(\tau_{\text{null}}\) to form a CI, taking care to set \(M\) to \(M_{\text{outcome}}+|\tau_{\text{null}}|\cdot M_{first-stage}\) for each value of \(\tau_{\text{null}}\) in the grid. The CI is formed by collecting the values of \(\tau_{\text{null}}\) in the grid for which the test fails to reject. Noack and Rothe (2019) provide an R package that does this automatically. To implement this functionality in the RDHonest package, one can code this grid and loop manually (please cite Noack and Rothe (2019) in addition to Armstrong and Kolesár (2018) if you are computing such an interval).

4 Extensions

This section discusses some options that are not directly supported by RDHonest-vStata. Some of these options are implemented in the R package or packages written by other authors, or can be implemented in the RDHonest package using some additional coding.

4.1 Clustered Standard Errors

Clustered standard errors are now included in the R package. While not yet available in the Stata package, one can run the rdhonest command to compute the worst-case bias. One can then run an equivalent regression using the regress command (restricting to a discontinuity sample or using weights corresponding to the bandwidth used by rdhonest) to get the same point estimate along with an option for clustering to obtain a cluster robust standard error. Note that this will give different results from the R package if the optimal bandwidth is used, since the R package uses a variance estimate that allows for dependence when computing the optimal bandwidth.

4.2 Additional Regressors

One may wish to include additional regressors, which can be interpreted as making a smoothness assumption on a partialled out outcome regressions, as discussed in Appendix B.1 of Armstrong and Kolesár (2018). Support for additional regressors is in progress.

4.3 Other Smoothness Classes

The smoothness class used by RDHonest-vStata assumes that the second derivative of the conditional expectation function on either side of the cutoff is bounded by \(M\). This is a Hölder smoothness class of order 2. Alternatively, once can use impose only an upper bound on the magnitude of the Taylor approximation, which leads to the Taylor or Sacks-Ylvisaker smoothness class. If the Taylor approximation comes from a second derivative bound, then this will be conservative, which is why the rdhonest Stata command uses the Hölder smoothness class. However, the Taylor/Sacks-Ylvisaker smoothness class is available in the R version of the package.

An alternative smoothness class based on an assumption that maximum error from a global polynomial approximation is taken away from the discontinuity point is used in Section IV.B of Kolesár and Rothe (2018). This class is not implemented in the RDHonest Stata package, but is available in the RDHonest R package. Note that the second derivative bound used by rdhonest corresponds to the smoothness class used in Section IV.A of Kolesár and Rothe (2018).

One may also want to consider higher or lower order smoothness (bounding a different derivative), or shape constraints. Kwon and Kwon (2020) consider the case of an monotonicity and bounds on the first derivative.

Formulas for minimax affine estimators using arbitrary convex smoothness classes based on convex programming are given in Donoho (1994) and Armstrong and Kolesár (2018). They can be implemented on a case-by-case basis using convex programming.

4.4 Multiple Bandwidths

The rdhonest command does not support different bandwidths on either side of the cutoff. This is motivated in part by calculations in Section D.1 of the supplemental appendix of Armstrong and Kolesár (2020), which show that there is little further efficiency gain from using different bandwidths on either side of the cutoff unless there is a very large jump in the conditional variance at the cutoff.

For fuzzy RD, the rdhonest command uses the same bandwidth for the first stage and reduced form outcome regressions. If the smoothness relative to conditional variance is substantially different in these regressions, one may wish to use different bandwidths. While this is not supported directly, one can run the first stage and reduced form outcome regressions as sharp RD specifications to obtain the maximum bias for each regression, which can then be plugged into the asymptotic formula given above. However, the variance formula will depend on the covariance of these estimates, and will need to be coded manually.

4.5 Fully Optimal Weights

Efficiency results in Armstrong and Kolesár (2020) show that the default triangular kernel used by rdhonest is 97.28% efficient among all possible weights in typical asymptotic settings. Nonetheless, one may gain some efficiency by numerically optimizing the weights, particularly with small samples and irregular design points.

Fully optimal weights were implemented by Armstrong and Kolesár (2018) for the Taylor class and are available in the R version of this package. For the Hölder class considered here, they are implemented by Imbens and Wager (2019) and available in the accompanying software package.

4.6 Efficiency Bounds

Armstrong and Kolesár (2018) derive efficiency bounds showing that the form of CI used by rdhonest (fixed length bias-aware CIs with optimized length) are near-optimal among all CIs. These finite-sample bounds depend on the design points, and can be computed on a case-by-case basis (although absolute bounds are also given). For the Taylor class, these efficiency bounds can be computed using the R version of this package. Asymptotic evaluations of these bounds with a continuous running variable do not depend on the distribution of the data; see Armstrong and Kolesár (2018) and Armstrong and Kolesár (2020).

4.7 Weak Instruments in Fuzzy RD

As discussed above, rdhonest can be used to compute a bias-aware version of an Anderson-Rubin style CI in fuzzy RD as proposed by Noack and Rothe (2019), although this requires manually looping over a grid of null values. The R package provided by Noack and Rothe (2019) does this automatically.

References